Testing cell renumbering:
In[7]:=
$Line=1234
Out[1234]=
1234
In[1235]:=
Range[10000]//Short
Out[1235]//Short=
{1,2,3,4,5,6,7,8,9,10,11,9978,9990,9991,9992,9993,9994,9995,9996,9997,9998,9999,10000}
Start with an image:
In[1]:=
img=
;
In[2]:=
dithered=[ColorConvert[img,"Grayscale"],2]
Out[2]=
Extract the set of coordinates corresponding to dark pixels with and add some slight noise:
In[3]:=
pts=PixelValuePositions[dithered,0];noisy=RandomReal[{-.15,.15},Dimensions[pts]]+pts
Out[4]=
Preview the points:
In[5]:=
Graphics[Point[noisy]]
Out[5]=
Use to generate a single line that visits very point:
In[6]:=
tour=Last[FindShortestTour[noisy]]
Out[6]=
These numbers represent the order that points should be visited. is a convenient way to represent graphics primitives using a set of points and indices.
Create a that passes through the points in order:
In[7]:=
Graphics[GraphicsComplex[noisy,Line[tour]]]
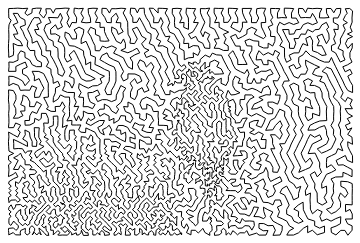
Out[7]=
Use the original image to add some color:
In[8]:=
Graphics[GraphicsComplex[noisy,Line[tour,VertexColorsDarker[RGBColor/@PixelValue[img,pts[[tour]]]]]]]
Out[8]=
Adding More Detail (2)
Adding More Detail
(2)
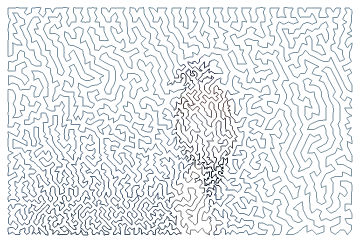
To add detail to the maze, all that's needed is to resize the image to a higher resolution. Similarly, the detail can be decreased by lowering the image resolution.
Double the resolution of the original image with :
In[1]:=
large=ImageResize
,Scaled[2]
Out[1]=
Repeat the steps from above:
In[2]:=
dithered=[ColorConvert[large,"Grayscale"],2];pts=PixelValuePositions[dithered,0];noisy=RandomReal[{-.15,.15},Dimensions[pts]]+pts;tour=Last[FindShortestTour[noisy]];Graphics[GraphicsComplex[noisy,Line[tour,VertexColorsDarker[RGBColor/@PixelValue[large,pts[[tour]]]]]]]
Out[6]=
Generalization (6)
Generalization
(6)